Bir koordinat sisteminden bahsettiğimizde, bir manifolddaki noktaların veya diğer geometrik elemanların yerini belirlemek için bir veya daha fazla sayı veya koordinatın kullanıldığı anlaşılır. Koordinatların sırası önemlidir ve “x-koordinatında” olduğu gibi konumlarına göre, bazen sıralı bir sıradaki sayılarla ve bazen de bir harfle tanımlanırlar. Koordinatlar, temel matematikte gerçek sayılar olarak ele alınır, ancak karmaşık sayılar veya değişmeli halka gibi daha soyut bir sistemin öğeleri olabilirler. Geometride, bir koordinat sisteminin kullanılması, problemlerin sayı problemlerine dönüştürülmesine izin verir ve bunun tersi de geçerlidir. Analitik geometrinin temeli budur.
Koordinat sistemleri:
Satır numarası:
Bir koordinat sisteminin en basit örneği, gerçek sayılarla bir doğru üzerindeki noktaları tanımlayan bir sayı doğrusu kullanılmasıdır. Bu sistemde, belirli bir satırda rastgele bir O orijini (orijin) seçilir. P noktasının koordinatları, O ve P arasındaki mesafe olarak tanımlanır. Spesifik mesafe, P noktasının hangi tarafının O orijin noktası olduğuna bağlı olarak pozitif (sağ) veya negatif (sol) olarak kabul edilir. Belirlenecek her nokta için , belirli bir koordinat belirtilir ve her gerçek sayı tek nokta biçimindedir.
Kartezyen koordinat sistemi:
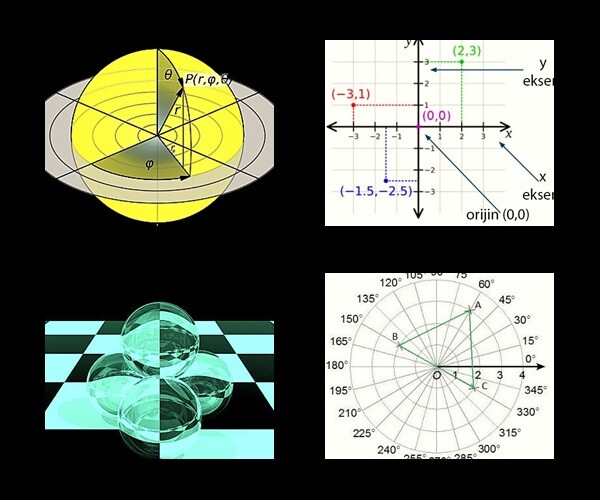
Tipik bir koordinat sistemi örneği Kartezyen koordinat sistemidir. Düzlem üzerinde birbirine dik iki doğru çizilir ve bir noktanın koordinatları bu doğrulara uzaklığına göre çizilir. Üç boyutta, üç seviye tanımlanır ve bir noktanın üç koordinatı, her seviye için belirli mesafelerle tanımlanır. Bu, n boyutlu Öklid uzayındaki herhangi bir nokta için n koordinat oluşturmak üzere genelleştirilebilir. Sistem, koordinat ekseninin yönüne ve düzenine bağlı olarak sağ veya sol yönlü bir sistem olabilir.
Kutupsala (Kutup) Koordinat Sistemi:
Bir uçak için başka bir koordinat sistemi kutupsal koordinat sistemidir. Kutup olarak bir nokta seçilir ve bu noktadan yayılan ışın kutup ekseni olarak alınır. Belirli bir θ açısında, θ açısı kutup ekseniyle olan kutuptan gelen bir çizgi (eksenden çizgiye saat yönünün tersine ölçülür) vardır. Bu doğru üzerinde orijin ile r arasındaki uzaklık (r sayısı için r olan) tek bir nokta ile işaretlenmiştir. Belirli bir koordinat çifti (r, θ) için yalnızca bir nokta varken, herhangi bir nokta birçok koordinat çifti ile temsil edilir. Örneğin, (r, θ), (r, θ + 2π) ve (r, θ +) aynı noktanın kutupsal koordinatlarıdır. Herhangi bir θ değeri için kutup noktası (0, θ) ile temsil edilir.
Silindirik ve küresel koordinat sistemleri:
Kutupsal koordinat sistemini üç boyuta genişletmenin iki yaygın yolu vardır. Silindirik bir koordinat sisteminde, kartezyen koordinatlarda olduğu gibi z koordinatları kutupsal koordinatlara r eklenir ve (r, θ, z) elde edilir. Küresel koordinatlar, bir çift silindirik koordinatı (r, z) kutupsal koordinatlara (ρ, φ) dönüştürerek üçgen koordinatlarla (ρ, θ, φ) bunu bir adım öteye taşır.
Homojen koordinat sistemi:
Düzlemdeki herhangi bir nokta, homojen koordinatlarda üçlü (x, y, z) ile temsil edilebilir. Burada x/z ve y/z noktanın kartezyen koordinatlarıdır. Bu, düzlemde bir noktayı belirtmek için yalnızca ikisinin gerekli olduğu “ekstra” bir biçimdir. Ancak bu sistem, bir izdüşüm düzlemi üzerindeki herhangi bir noktayı sonsuzluk kullanmadan gösterdiği için kullanışlıdır. Genel olarak, homojen bir koordinat sistemi, gerçek değerlerin değil, yalnızca koordinatların oranlarının önemli olduğu bir sistemdir.
Diğer koordinat sistemleri:
Çeşitli alanlarda yaygın olarak kullanılan tüm koordinat sistemleri burada açıklanamayacağından, bazılarından kısaca bahsedeceğiz:
– Eğrisel koordinat sistemi: Koordinat sistemlerinin genelleştirilmiş halidir ve sistem eğrilerin kesişmesine dayanır.
– logaritmik – kutupsal koordinat sistemi: düzlemdeki bir noktayı, orijine olan uzaklığının logaritması ve orijinin kesiştiği bir referans çizgisinden ölçülen açı ile belirtir.
– Julius Plücker koordinatları: üç boyutlu Öklid uzayındaki çizgiler, homojen koordinatlar olarak altı basamaklı değişkenler kullanılarak gösterilir.
Genelleştirilmiş koordinatlar: Klasik mekaniği yeniden formüle eden Joseph Louis Lagrange’ın yönteminde kullanılır.
Kanonik koordinat sistemi: Hamiltonyen’deki mekanik işlemler için kullanılır.
Barisentrik koordinatlar: trigonometrik grafiklerde ve daha genel olarak trigonometrik analizde kullanılır.
Geometrik eleman koordinatları:
Koordinat sistemleri genellikle bir noktanın yerini belirtmek için kullanılır. Ancak çizgiler, düzlemler, daireler veya küreler gibi daha karmaşık şekillerin konumunu belirtmek için de kullanılabilirler. Örneğin, uzayda bir çizginin konumunu belirlemek için Plücker koordinatları kullanılır. Gereksinimlere göre, açıklanan şekil, koordinat sisteminin türünü ayırt etmek için kullanılır.
Bazen iki farklı geometri grubu için, farklı koordinat sistemleri analizleri açısından eşdeğer olabilir. Bunun bir örneği, projektif düzlemdeki noktaların ve çizgilerin homojen koordinat sistemleridir. Böyle bir durumla karşılaşıldığında iki sistemin dual olduğu söylenir. İkili sistemler bir sistemden diğerine geçme yeteneğine sahiptir, çünkü söz konusu sonuçlar aynı analitik sonucun basitçe farklı yorumlarıdır ve buna dualite ilkesi denir.
Transferler:
Farklı koordinat sistemleri için genellikle birçok olasılık olduğundan, geometrileri tanımlamak için ilişkilerini doğru bir şekilde anlamak önemlidir. Bu ilişkiler, bir sistemdeki koordinatlar için başka bir sistemdeki koordinatlar cinsinden formüller verebilen koordinat dönüşümleri ile belirlenir. Örneğin, bir düzlemde Kartezyen koordinatlar (x, y) ve kutupsal koordinatlar (y,) aynı orijine sahipse ve kutupsal eksen pozitif x ekseni ise, o zaman koordinatların kutupsal koordinatlardan kutupsal koordinatlara dönüşümü (x = r cosθ) ve (y = r sinθ)) görüntüde olacaktır.
İki koordinat kayması, her önyargıyla ilişkilendirilebilir.
Her noktanın görüntüsünün yeni koordinatları, noktanın eski koordinatlarıyla aynıdır (Mapping’deki formüller, Transform’dakilerin tersidir). Ve her noktanın görüntüsünün eski koordinatları, noktanın yeni koordinatlarıyla aynıdır (eşlemedeki formüller dönüşümdeki ile aynıdır).
Doğrular/eğriler ve düzlemler/koordinat yüzeyleri:
İki boyutta, koordinat sisteminde bir koordinat sabit kalır ve diğer koordinatların değişmesine izin verilirse, ortaya çıkan eğriye koordinat eğrisi denir. Kartezyen koordinat sisteminde, koordinat eğrileri aslında düz çizgilerdir, dolayısıyla koordinat çizgileridir ve özellikle koordinat eksenlerinden birine paralel çizgilerdir. Diğer koordinat sistemlerinde, koordinat eğrileri genel eğriler olabilir. Örneğin, bir r sabitine basılarak elde edilen kutupsal koordinatlardaki koordinat eğrileri, orijinde merkezli dairelerdir. Öklid uzayı için Kartezyen koordinat sistemi dışındaki koordinat sistemlerine eğrisel koordinat sistemleri denir. Ancak bu her zaman böyle değildir, örneğin homojen bir koordinat sisteminde koordinat eğrileri bulunmaz.
Üç boyutta, bir koordinat sabit tutulurken diğerlerinin değişmesine izin verilirse ortaya çıkan yüzeye koordinat yüzeyi denir. Örneğin, küresel bir koordinat sisteminde ρ sabit tutularak elde edilen koordinat yüzeyleri, orijinde merkezli kürelerdir. Üç boyutlu uzayda, bir yüzeyin kesişimi, bir koordinat eğrisinin koordinat yüzeyidir.
Harita Formatı:
Bir koordinat haritası kavramı, manifoldlar teorisinin merkezinde yer alır. Bir koordinat haritası, her noktanın belirli bir alanın bir alt kümesi için bir dizi koordinat içerdiği bir koordinat sistemidir. Daha kesin olarak, koordinat haritası, X uzayının açık bir alt kümesinden Rn’nin açık bir alt kümesine benzerliktir. Tüm alan için tutarlı bir koordinat sistemi bulmak genellikle mümkün değildir. Böyle bir durumda, alanı kapsayacak bir atlas oluşturmak için koordinat haritaları bir araya getirilir. Böyle bir atlasın bulunduğu uzaya manifold adı verilir ve eğer koordinat haritaları birbiriyle uyumlu ise bu manifold üzerine ek bir yapı yerleştirilebilir.
Oryantasyona dayalı koordinatlar:
Geometri ve kinematikte, koordinat sistemleri yalnızca noktaların doğrusal konumunu tanımlamak için değil, aynı zamanda eksenlerin, düzlemlerin ve katı cisimlerin açısal konumunu da açıklamak için kullanılır. Örneğin, rijit bir cismin oryantasyonu, üç sütunundaki üç noktanın Kartezyen koordinatlarını içeren bir oryantasyon matrisi ile temsil edilebilir. Bu noktalar, sistem eksenlerinin yönünü belirlemek için kullanılır.
Kaynak:
– Luther Pfahler Eisenhart, “Koordinat Geometrisi”, Dover Publications Inc., (2005).
— MI Voitsekhovskii, A. B. Ivanov, “Coordinates,” Encyclopedia of Mathematics içinde, Springer Science & Business Media BV/Kluwer Academic Publishers, (2001).
yazar: Juni Saraoğlu’nu aç
Diğer gönderilerimize göz at
[wpcin-random-posts]